Project Navigator:
Project Navigator is a set of astrodynamics and interplanetary navigation software that I have written. There used to be an old C++ version of this, back in 2010, but the newer Matlab version has updated algorithms, and better visualization capabilities.
The purpose of this software is to perform interplanetary trajectory calculations for the purpose of mission analysis and design. The software has a two-body dynamic heirarchial and extensible solar system model, populated with orbit element sets from JPL's solar system dynamics group's website. This software has routines for solving the UTOF problem and classical two-impulse Gauss problem, using algorithms from Bate, Mueller, and White's Fundamentals of Astrodynamics.
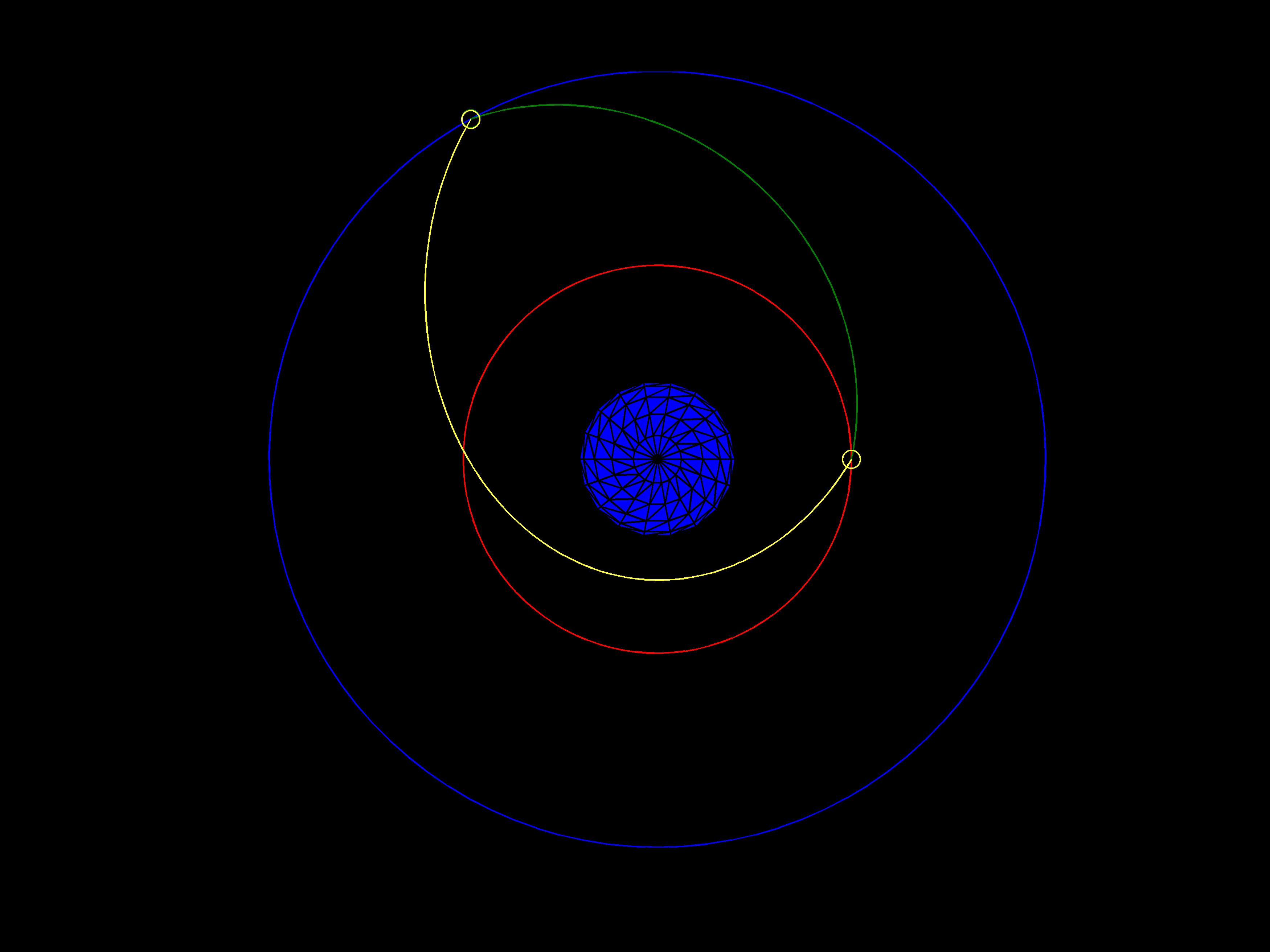
The two orbit-arc solutions to the classical Gauss problem for Earth Orbit transfer.
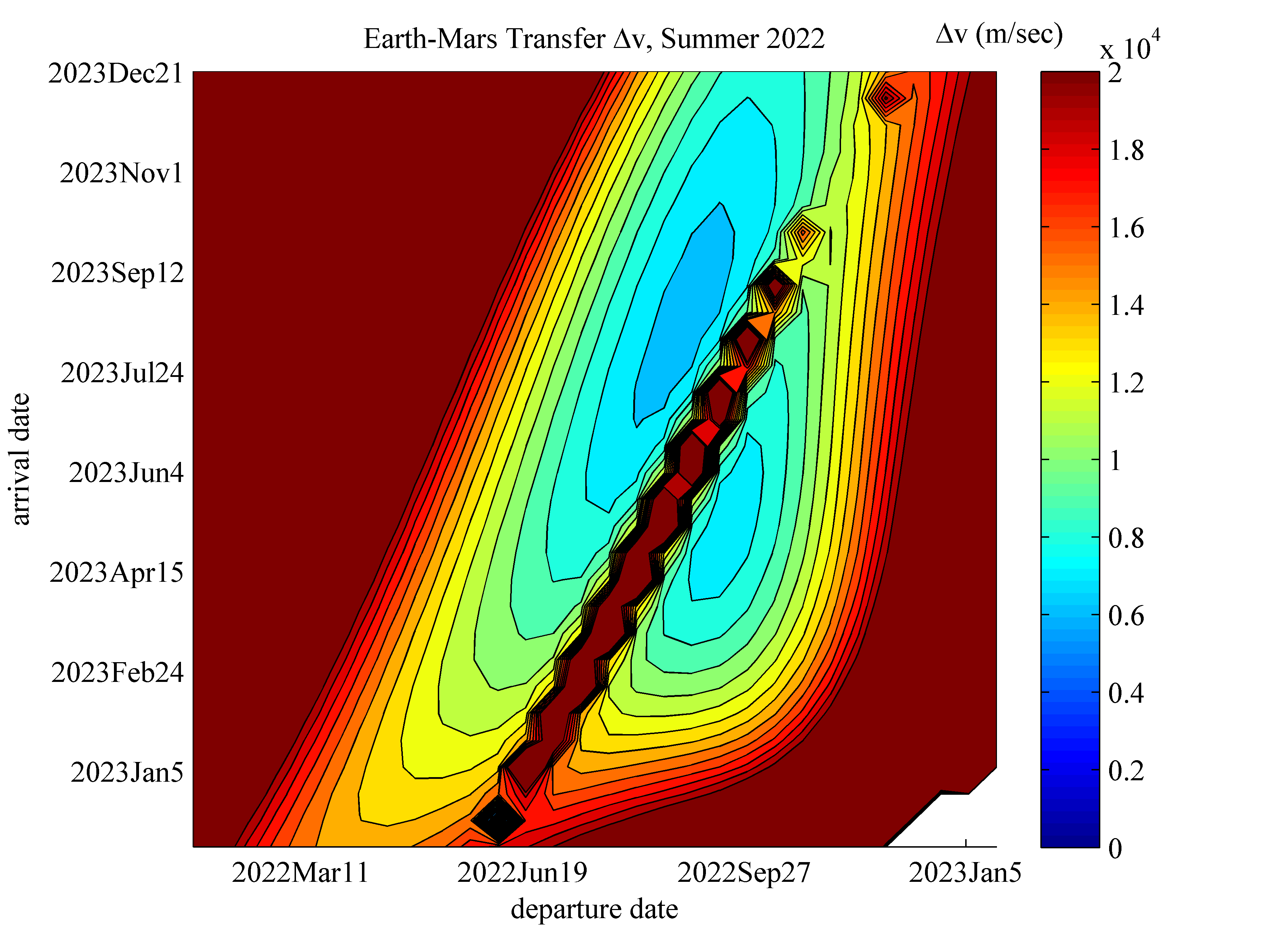
A "porkchop plot" showing two-impulse transfer Delta-Vs for an Earth-to-Mars mission departing in Summer 2022.
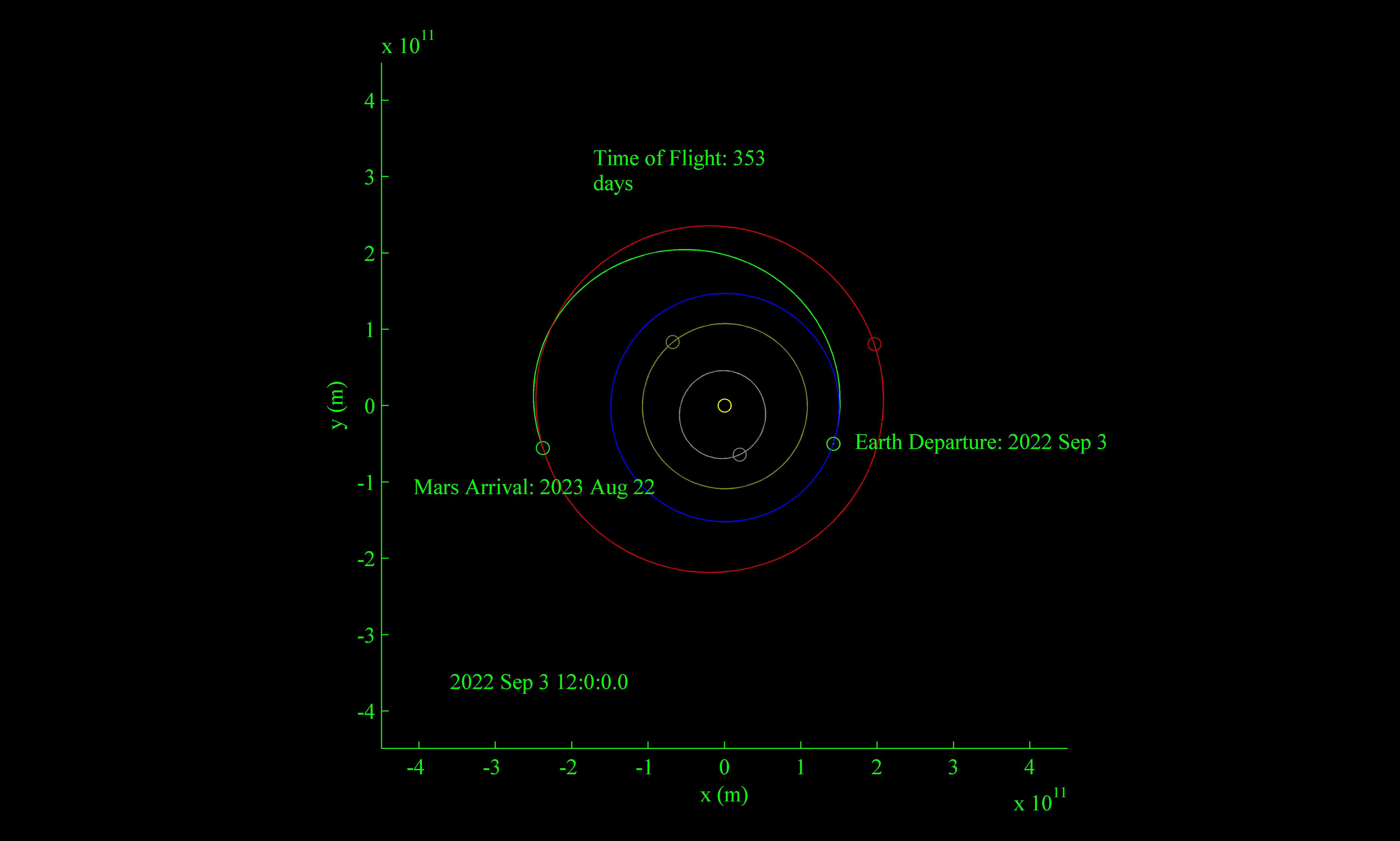
An Earth-to-Mars type II trajectory.
New features added to the code recently include a suite of constrained and unconstrained optimization routines that act on general objective functions to minimize them according to constraints. Algorithms used include Conjugate Gradient descent, Newton-Rhapson, Newton-Rhaphson solving the augmented lagrangian for a constrained optimization problem, Newton-Rhaphson using Broyden-Fletcher-Goldfarb-Shannon (BGFS) to approximate a Hessian, and others
The optimization routines allow for the optimization of low thrust trajectories. This enables analysis of the flexibility and mass requirements for EP propelled interplanetary missions.
Features:
- Translates freely between position and velocity, and Keplerian orbit element sets
- Solves for future position and velocity given current position and velocity, or orbit elements at an epoch using the universal variables formulation.
- Solves the Gauss Problem (given an initial and final position and time of flight, find the two orbits that meet those conditions.)
- Generates porkchop plots for interplanetary patched-conic transfers. Used for launch window and delta-V prediction.
- Solves optimization problems using CG linesearch to optimize low-thrust interplanetary trajectories.
Low Thrust Trajectory Optimization
Importance of High Isp in Interplanetary Flight
Rockets are governed by Tsilkovsky's rocket equation, which relates the mass fraction of propellant that a spacecraft must expend to the delta-V of the maneuver that a spacecraft intends to make and the exhaust velocity of the propellant jet. The higher the jet exit velocity, the more efficiently the spacecraft can make a given transfer between orbits. This is an exponential relationship, so large delta-Vs require either very large propellant-mass-fractions for the spacecraft (becoming impractically large very quickly for chemical propulsion), staging, or higher jet speeds from the engine.
For historical reasons (related to solid rocket testing), propellant jet speed is measured in terms of Isp, or internal specific impulse. Isp is the jet speed divided by the acceleration due to Earth's gravity at Earth's surface. A typical Isp for a LH2/LOX chemical rocket would be 400 sec. For a solid rocket, it would be ~250 sec.
Spacecraft rocket engines can be broadly divided into classes based on where the energy to accelerate the propellant comes from. Chemical rockets are powered by chemically reacting the propellant. The specific energy of the chemical reaction limits the specfic energy of the propellant jet, and hence the Isp attainable by these rockets. The propellant choice, within very narrow limits, defines the Isp, which is seldom higher than 450 sec in vacuum. Nuclear thermal rockets are a promising technology for massive interplanetary vehicles. These rockets use a nuclear reactor to heat a low molecular mass (usually hydrogen) propellant, and can acheive higher Isps than chemical propulsion. For nuclear propulsion, the limiting factor is the reactor temperature. Historical tests of nuclear thermal rockets have achieved Isps of 850 sec [ref]. These Isp limitations mean that, for interplanetary missions, where total delta-Vs of 10s of km/sec are not unusual, large propellant mass fractions or staging are required for the spacecraft.
Electric propulsion systems differ from chemical rockets in that an external electric power source is used to accelerate a propellant. Accleration is usually acheived by ionizing the propellant and manipulating it via electric and magnetic fields. The external nature of the power source means that any amount of specific energy desired can be added to the propellant, enabling much higher Isps to be obtained. Ion drives can operate in the range of 2500 to 4000 sec Isp. Hall effect thrusters (HETs) have historically operated between 1500 and 2000 sec. For a fixed power limit, there is a tradeoff between thrust and Isp. Current electric propulsion devices have been designed for missions with only a few kW of power, so thrusts tend to be low. Thrusts on the order of 100 - 300 mN for ion drives, and 80-300 mN for Hall thrusters are typical. [refs]
Future missions carrying people or cargo may use higher power propulsion schemes such as magneto-plasmadynamic rockets (MPDs) or designs such as VASIMR (which uses a magnetic nozzle to confine plasma which is heated by an RF anyenna). For VASIMR, 200 kW thruster powers have been achieved in the lab, for Isps of 3500 sec, at efficiencies of 0.54.
Importance of Low-Thrust Trajectory Optimization
Missions using high-thrust propulsion, such as chemical or nuclear thermal rockets, can be designed using simple patched-conic approximations, where a small number of 'impulsive' burns (short burns relative to the dynamics of interplanetary orbits) can be planned to place the spacecraft onto transfer orbits linking the departure and destination.
Even future high power electric propulsion missions will have low thrusts relative to the mass of the spacecraft. The acceleration time is on the same order as the time of flight. To design trajectories for these vehicles, trajectory optimization routines to solve for the acceleration histories are necessary.
Completed Current Work
Project Navigator now has two low-thrust trajectory optimization routines to solve for low-thrust trajectories and thrust control for interplanetary missions.
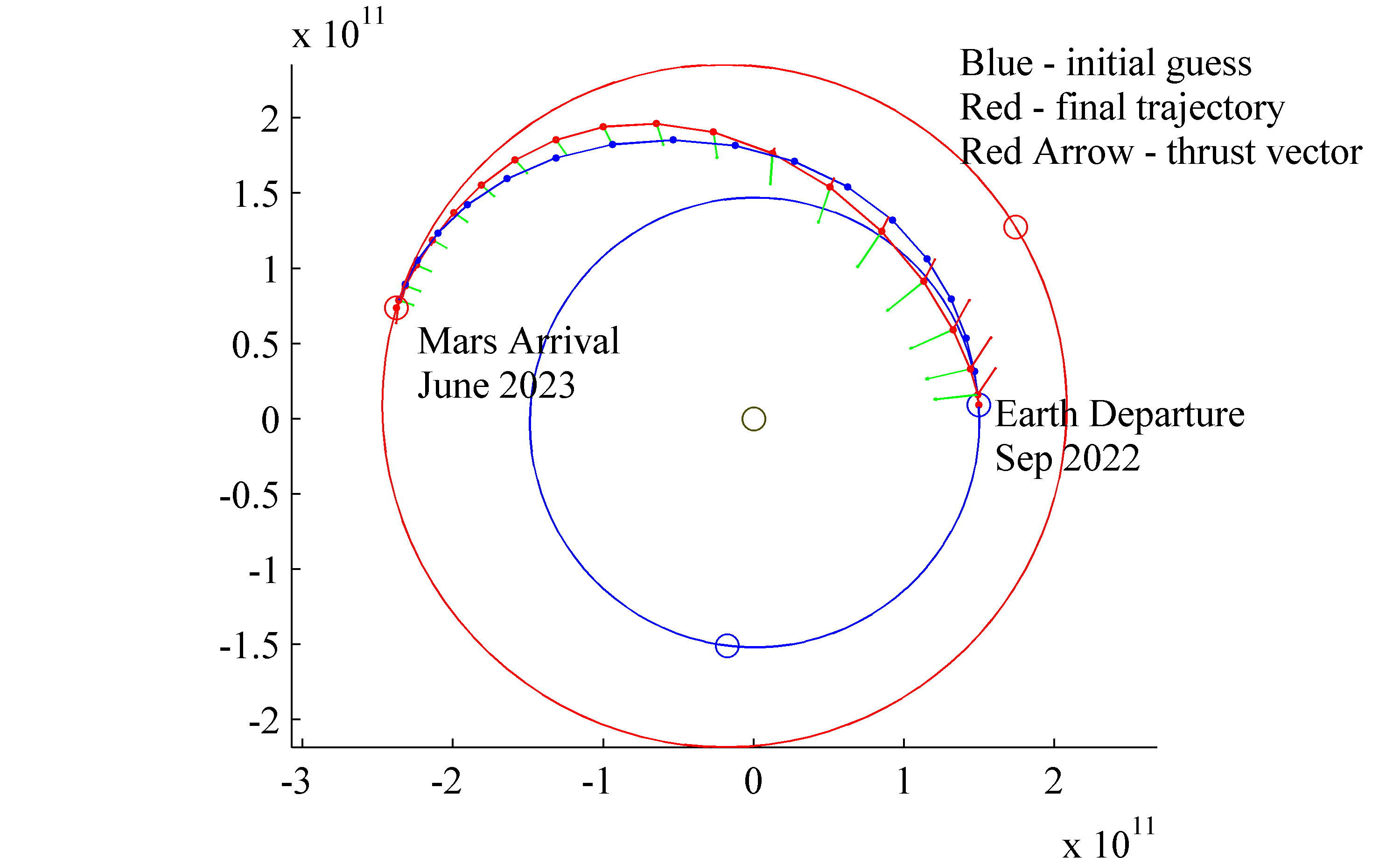
Low thrust trajectory optimizer using spline control points as optimization parameters.
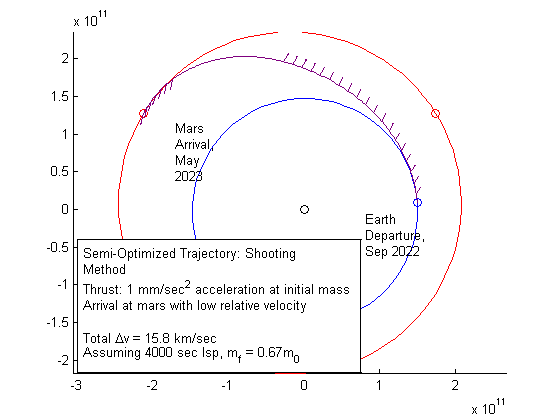
Low thrust trajectory using fixed thrust, shooting method, using conjugate-gradient line-search to minimize an augmented objective function. The objective function enforces the boundary conditions and penalizes delta-V
The following two figures are from a trade study comparing a two-impulse Earth-Mars mission beginning on 1 Aug 2022 with two low-thrust scenarios. The first series (blue circles) are missions with 3000 sec Isp engines, with a 1 mm/sec^2 acceleration capability at the initial spacecraft mass (thrust/initial mass). The second series (blue diamonds) is the same physical scenario run with twice as many timesteps and more control points for thrust pointing (to verify that I'm actually close to convergence, and the Pareto front). The third series (green diamonds) is the same scenario, but with half the thrust capability (1 mm/sec^2 is an ambitious acceleration capability for EP, but within the realm of engineering possibility. 0.5 mm/sec^2 is closer to current missions.)
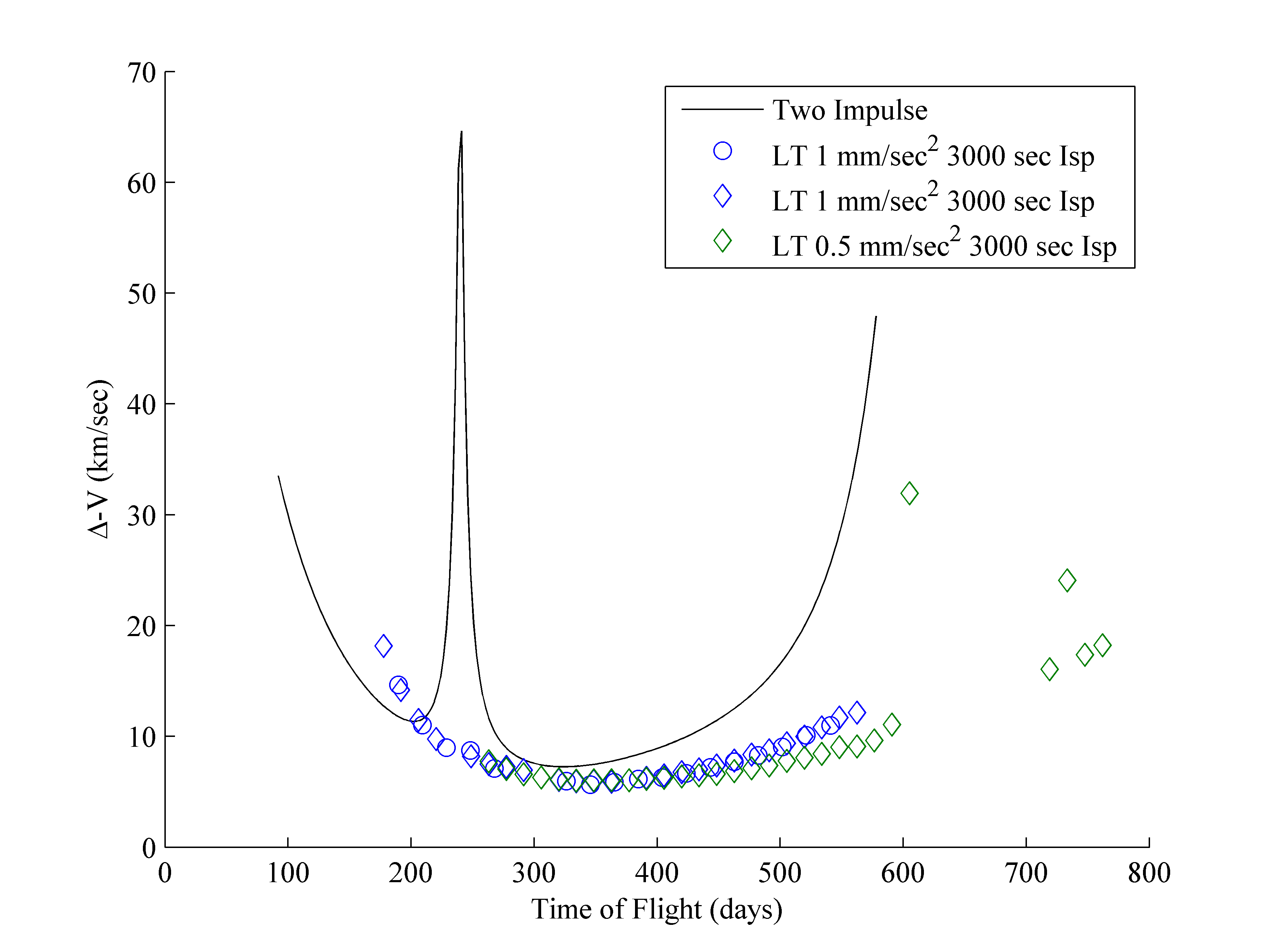
Delta-V for two-impulse high thrust trajectory compared with delta-Vs for low thrust trajectories at different times of flight. The low-thrust trajectories are able to converge after about 180 days of flight for the 1 mm/sec^2 case, and 250 days for the 0.5 mm/sec^2 case. The delta-Vs are not much worse, and for long flight times are better, than for the two-impulse trajectories.
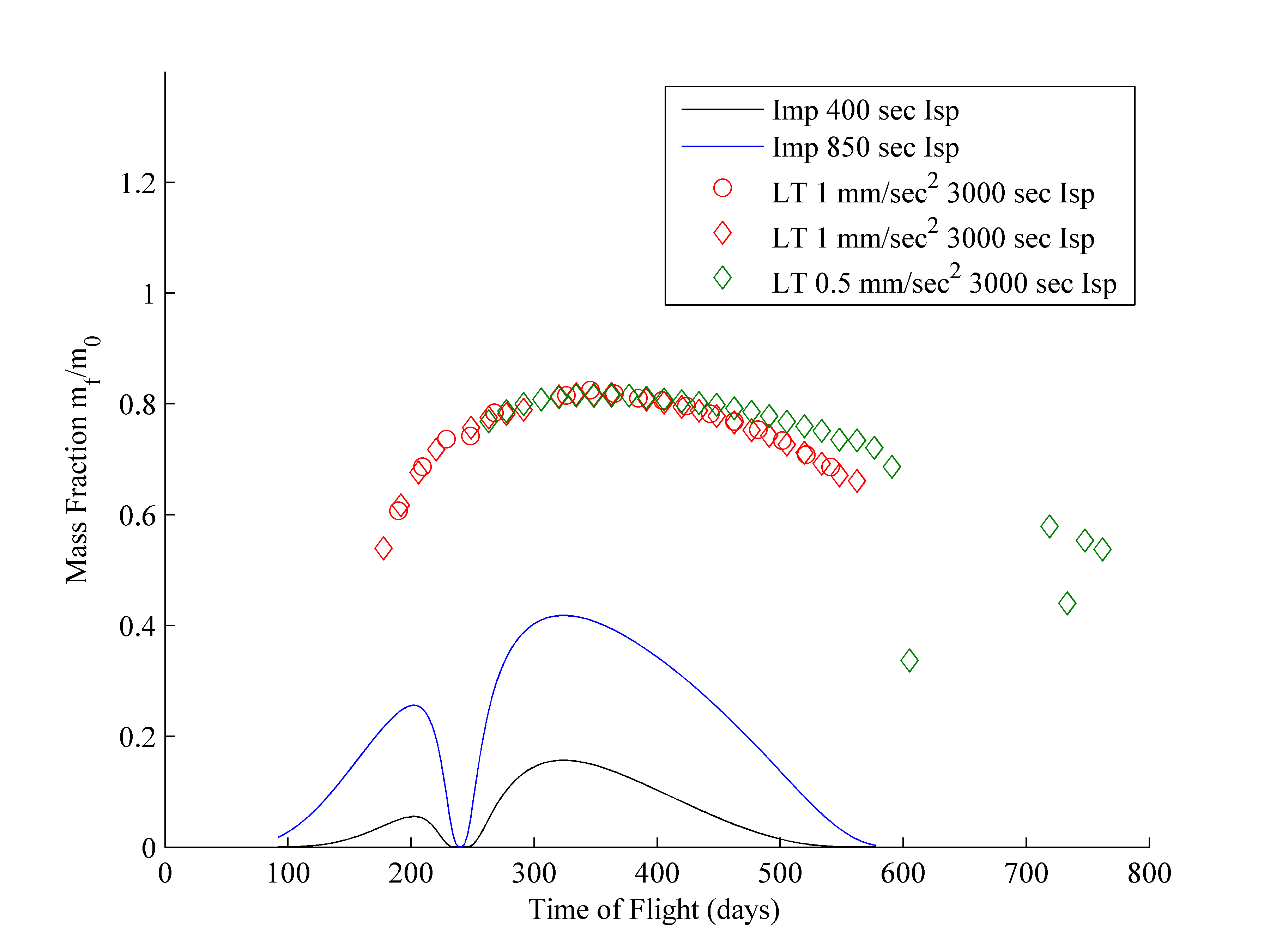
This shows the mass fraction for high-thrust engine Isps (chemical and nuclear thermal) for the impulsive trajectories and the mass fractions assuming a low-thrust engine with 3000 sec Isp.
As you can see, while travel times are longer for lower thrusts (within the range of the slower Type-II trajectories for impulsive maneuvers for 1 mm/sec^2, a little longer for 0.5 mm/sec^2), the *compelling* advantage of using EP for main propulsion is the far higher mass fractions attainable. Even for a nuclear thermal rocket (850 sec Isp, ref: [insert later - ROVER/NERVA]), the best you can do for a *one way trip* is a mass fraction of 0.5 or so. For a two way trip, 75% or more of your vehicle would have to be propellant. If you use a low-thrust, but high Isp EP engine, 60-80% of your vehicle can be useful payload and structure.
Licensing Stuff:
The project report paper is copyright Aaron M. Schinder, 2016. Contact me if you are curious about it.
The project code, when I get around to commenting it and cleaning it up, will be released under the BSD license.
LICENSE: BSD License
Copyright (c) 2016, Aaron M. Schinder
All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
|