Disclaimer: This is my personal blog. Any opinions presented here are personal opinions, not affiliated with my professional work. All work shown here was done on my own time with personal resources.
Elon Musk made a speech at the International Astronautical Congress outlining SpaceX’s goal for the sort of vehicle they want to build as part of their Mars plan.
It’s here on Youtube. https://www.youtube.com/watch?v=IFA6DLT1jBA
I would recommend watching it: It’s an interesting presentation. Only partially flashy imagery, it contains some technical details about their mission idea and what they are working on to build up to it.
The vehicle described is an extremely large, extremely lightweight (for the size and propellant mass) vessel. It has to be to have a chance of doing what it is proposed to do (fly from LEO to Mars with only a single chemically-propelled stage). (The goal is for the booster to have only 4% inert mass!) Needless to say, there will be a great many engineering challenges to build the vehicle described in the presentation. It will be interesting to see exactly how far composite construction can be pushed, and if these mass-fractions can be attained, much less result in a vehicle that can withstand aerobraking (not just at Mars, but returning to Earth). It will be interesting to see if the problem of pushing a very large vehicle with a great many rocket engines can be solved. (You get noise problems either way: With many small engines, or with a few very large engines.)
But how does it hold up on the basic physics? One of the things that caught my eye during the presentation were the extremely short travel times to Mars. Chemically propelled spacecraft and probes usually launch from Earth at specific times, coast to Mars, and enter Mars at specific arrival times to minimize the delta-V, which governs the propellant cost of the mission. Mass margins on chemically propelled rockets are tighter than a swiss watch, and no one launches outside of certain very narrow minimum delta-V launch windows. These windows, for both type I and type II trajectories tend to result in times of flight much longer than 80 to 100 days: Usually 8.5 months is given as a ballpark. Somewhere between 200 days and a full year.
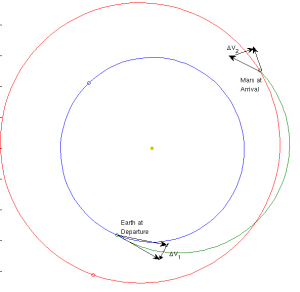
This is an example of a transfer orbit. It isn’t a good one, but it is plotted for example’s sake to show where you maneuver and how to get from Earth to Mars.
This is an example of a “porkchop plot”, which shows totally propulsive delta-V’s for Earth-Mars transfers. It shows the delta-V as a function of departure and arrival times.
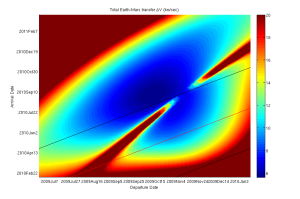
Porkchop plot for Earth to Mars, total Delta-V, 2009 departures. The three lines are 100, 200, and 300 day travel times respectively.
This bothered me, because SpaceX is a rocket company. They can’t not understand orbital mechanics and do what they do. It would be highly incongruous to design a rocket, and mess up the orbital mechanics – which is where the design of space missions tend to start! So, odds are they aren’t pulling numbers out of nowhere. But what assumptions are they making that let them do that?
I think I’ve figured out some of what you would have to assume to actually get those transit times.
First: The upper-stage spaceship: The desired inert mass, propellant mass, and thruster Isp are given. These determine how much delta-V the spacecract can develop before it runs out of fuel. Tsilkovsky’s rocket equation gives the following.
(m_final/m_total) = (1-m_prop/m_total) = exp(- delta-V/v_e)
With 450 tons of cargo, the vehicle only has 5.4 km/sec of delta-V. The spacecraft has to make several maneuvers to reach Mars.
1. It has to escape from Earth from the starting orbit.
2. It has to thrust to transfer from a near-Earth solar orbit to a Mars-Transfer orbit.
3. It has to somehow enter a Mars orbit from the transfer orbit (more on this later).
4. It has to land on the surface propulsively.
To escape Earth from LEO, you need 3.25 km/sec of delta-V. This only leaves 2.1 km/sec left over. This isn’t enough to make the transfer to Mars from even the most favorable conditions on even the slowest of trajectories.
Suppose you don’t carry the full load of cargo though: If the vehcile was only carrying 100 tons, then it has 8.1 km/sec, which leaves 4.8 km/sec of delta-V left over after escape. This could enable the vehicle to make some of the easier transits and still have a tiny bit of delta-V left over for landing.
How does the vehicle get off the transfer orbit, into Mars orbit, and land? This mission concept must assume that all the delta-V on Mars entry is taken care of by aerobraking. The vehicle will be significantly lighter when it reaches mars, and so might have some advantages there: Large surface areas and low mass gives a ballistic coefficient that <i>might</i> allow it to shed both the transfer orbit velocity (dV2) and the velocity it will pick up by falling into Mars’s gravity well (about 4.9 km/sec). The delta-V’s for aerobraking for the short travel times can be quite high though: 5 + anywhrere from 5-10 km/sec for these faster orbits. I’ll have to think about how the thinner atmosphere will change things. (For reference, the EDL stage of the Curiosity lander hit the Martian atmosphere at only ~5 km/sec. It must have matched the solar-orbit speeds with Mars very well at the end of it’s transfer, which you can only do with low-energy transfer orbits.)
Propulsive landing: You want some delta-V to make the landing. 1000 m/sec is a pretty tight margin, especially since Mars gravity is higher than the moon’s. You don’t have to deal with propulsively canceling orbital speeds, but you do have to apply positive control to land and stop falling.
But how would you do it in 80 days? Suppose instead of escaping Earth from LEO, you launch into a near-escape elliptical orbit. Tankers would have to follow the vehicle around on the elliptical orbit and fill it there. When the vehicle reaches perigee, it can make a small delta-V to escape Earth, and have most of the delta-V left over for Mars transfer and landing.
Below are some plots: They are plots of the “launch windows” between Earth and Mars, in terms of delta-Vs. They are the porkchop plots from before, but skewed 45 degrees to be put in terms of transit time. The first is the Earth to Mars tranfer delta-V. This is the only one the spaceship would be making. The second is the Mars-Transfer to Mars solar orbit delta-V. This, plus ~5 km/sec is what you need to shed on aerobraking. If you were trying to enter a controlled orbit about Mars, you would need to spend the total delta-V (third plot), and maneuver in Mars orbit (with some ability to finesse due to gravity capture, etc).
So ~100-120ish days isn’t outside the realm of physical possibility after all, if you can aerobrake away your Mars entry delta-V, and if you take less cargo, and if you launch from a high Earth orbit instead of a low Earth orbit… Okay, so it is a little crazy: It has absolutely no margin for error. But it’s not impossible.
(PS 450 tons, 100 tons – these are very large masses relative to anything we fly today, but what matters in interplanetary flight is the mass relative to the propellant (landing is another matter). The vehicle is stated to have 150 tons of inert mass, 1950 tons of propellant, and up to 450 tons of cargo. The Isp of the engines is 387 sec, giving 3743 m/sec of jet exhaust velocity.)
For reference:
Earth escape starting from LEO: 3.4 km/sec
Earth escape starting from near Earth but not orbit: 11 km/sec (also what you pick up when you return to Earth and fall into it’s gravity well. A very heavy re-entry loading seen during Apollo.)
Mars entry (or escape) from the surface: 5 km/sec
Mars entry (or escape) from low Mars orbit: 1.45 km/sec
Typical total Earth to Mars transfer delta-V given that it is minimized (leads to 200+ day travel time): 5.5-8 km/sec.
For playing with the travel times and launch dates, see the plots above:
Also, these plots assume you are only doing a two-impulse maneuver. Trajectories with fly-bys, or trajectories with 3 or more impulses, or low-thrust trajectories require solving optimization problems.



Recent Comments: