« Archives in February, 2011

I can has manifold calculus

February 18, 2011 / posted in Uncategorized / 2 Comments

No. I’m not crazy. Not quite yet. Hehehehe.

I’ve been trying to work with manifold calculus over the past few days, working up to a general understanding of partial differential equations in arbitrary coordinate systems. Differential operators can end up doing some freaky things if your coordinate system isn’t orthonormal.

I’ve also been going through Grassman/Clifford algebra and it’s relation to strictly anti-symmetric tensors. I think I’ve got that roughly down, but the algorithm for evaluating their measure, while it looks pretty elegant in it’s compact form, is not at all nice to compute, or simplify.

Hopefully, once I can get this all down to the point where I can understand it, certain other aspects of things like reletavistic electrodynamics will become clearer.

Still, slow going.

Victory is mine!!! !! !

February 3, 2011 / posted in Programming / 1 Comment

Finally! I managed to figure out what I was doing wrong. When I calculated the orbital positions on the plane, I was measuring both the perigree axis and the true anomaly from the same reference axis (called k1, 90 degrees from the axis of the ascending node). This was incorrect – in the 3d case I was measuring the true anomaly from the perigree axis, as I was supposed to. Just one tiny change, and now everything works!


Edge cases are evil!

February 2, 2011 / posted in Programming / No Comments

So, I’m in the middle of putting together a bunch of code under a project called “Project Navigator”. Navigator is supposed to help me perform astrodynamics calculations.

While the math involved has been easy, the programming has been a nightmare. Why? Edge cases. I don’t know how many times I thought I was almost done, only to have some obscure numerical condition come up to bite me. If there are hyperbolic transfers, I need code to handle all the period counters to make sure I don’t wander off to infinity in a finite time. I also need to be able to integrate clockwise and counterclockwise around the conic section without bridging any critical angles.

My prior attempt at solving for transfer orbits attempted to avoid all this minutia by running a generalized solver to fit one conic section to bridge the departure and arrival points of the other two. Unfortunately, there are all sorts of perverse local minima lurking in configuration space which my solver delighted in bombing out on. It was also waaay to slow.

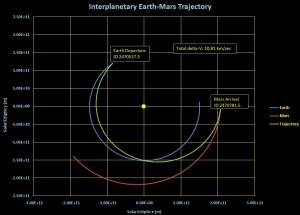
Okay, so I did some math and worked through everything on the plane with only one variable. I finally managed to beat all those problems into submission. Only I didn’t. When I tried to map the projected orbit back into three dimensions, I discovered that there was something screwed up about the projection – now there *are* no angles I can pick to match the transfer plane to the departure and arrival points, and I have no idea why, because I quadruple checked my rotation matrices and angle math.

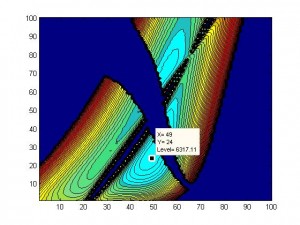
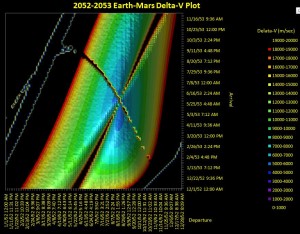
I attempted a C3 plot of the delta-v for departure to Mars. See that blob? It’s supposed to be relatively contiguous, with two minima. Instead it is cut up, folded over, and scattered all over the plot.

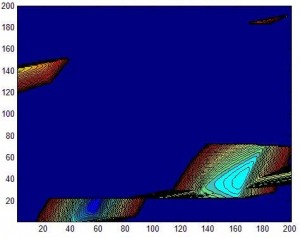
Gaah!

I spent an entire week trying to *fix* all the bugs. At this point I’m not learning anything new, I’m just bogging down trying to find out why the code is blowing up.

The most galling thing is that none of this *should* be difficult. It shouldn’t require 4000 lines of code, it shouldn’t need 15 levels of nested if statements to handle everything that goes wrong. I can solve these cases by hand faster than I can via computer!

I’ll take a break, but won’t give up on the project entirely. I seem to have made a few key corrections. It looks (jinx) like I am approaching the end of the fatal bugs.